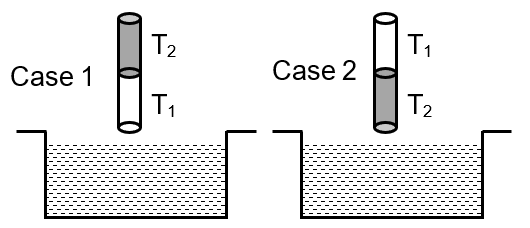
A cylindrical capillary tube of 0.2 mm radius is made by joining two capillaries T1 and T2 of different materials having water contact angles of 0° and 60°, respectively. The capillary tube is dipped vertically in water in two different configurations, case I and II as shown in figure. Which of the following option(s) is(are) correct ?
(Surface tension of water = 0.075 N/m, density of water = 1000 kg/m3, take g = 10 m/s2)
Know your College Admission Chances Based on your Rank/Percentile, Category and Home State.
Get your JEE Main Personalised Report with Top Predicted Colleges in JoSA
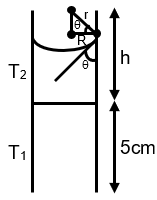
⇒ h1 = 75 mm (in T1) [If we assume entire tube of T1]
⇒ = 37.5 mm (in T2) [If we assume entire tube of T2]
Option (A) : Since contact angles are different so correction in the height of water column raised in the tube will be different in both the cases.
Option (B) : If joint is 5 cm is above water surface, then lets say water crosses the joint by height h, then:
= P0
⇒ h = –ve, not possible, so liquid will not cross the interface, but angle of contact at the interface will change, to balance the pressure,
So option (B) is wrong.
Option (C) : If interface is 8 cm above water then water will not even reach the interface, and water will rise till 7.5 cm only in T1, so option (C) is right.
Option (D) : If interface is 5 cm above the water in vessel, then water in capillary will not even reach the interface. Water will reach only till 3.75 cm, so option (D) is right.