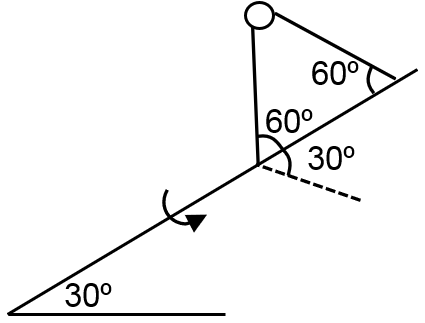
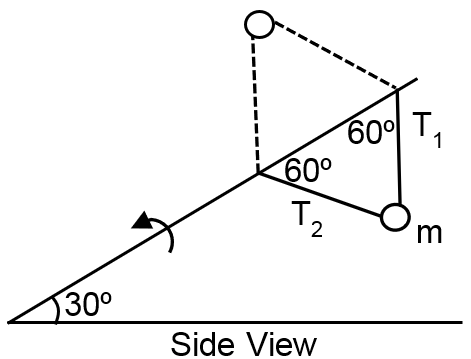
A rod is arranged at an angle of 30° from the horizontal. Attached to the rod with two strings is the mass m, as shown. The rod is rotated, maintaining its direction in space, so that m travels in a circular path. The strings are of equal length , and make angles of 60° with the rod as shown. Take the length of the strings as 2.4m. Calculate the minimum value of the tangential speed (in m/s) of the mass such that the string with tension T2 does not become slack when the mass is directly above the rod.
Know your College Admission Chances Based on your Rank/Percentile, Category and Home State.
Get your JEE Main Personalised Report with Top Predicted Colleges in JoSA
r = cos 30° =
T2 cos 30° + T1 cos 30° + mg cos 30° =
T2 sin 30° + mg sin 30° = T1 sin 30°
Just slack ⇒ T2 = 0° ⇒ T1 = mg
2mg cos 30° × L cos 30° = mv2
v2 = 2 × L × 10
v2 = × 10 × 2.4 = 36 ⇒ v = 6m/s