An isosceles right angled triangle whose sides are 1, 1, lies entirely in the first quadrant with the ends of the hypotenuse on the coordinate axes. If it slides prove that the locus of its centroid is (3x - y)2 + (x - 3y)2 = .
Know your College Admission Chances Based on your Rank/Percentile, Category and Home State.
Get your JEE Main Personalised Report with Top Predicted Colleges in JoSA
b = cosθ a = sinθ
∴ C'
x = 1 . cos(135° – θ) =
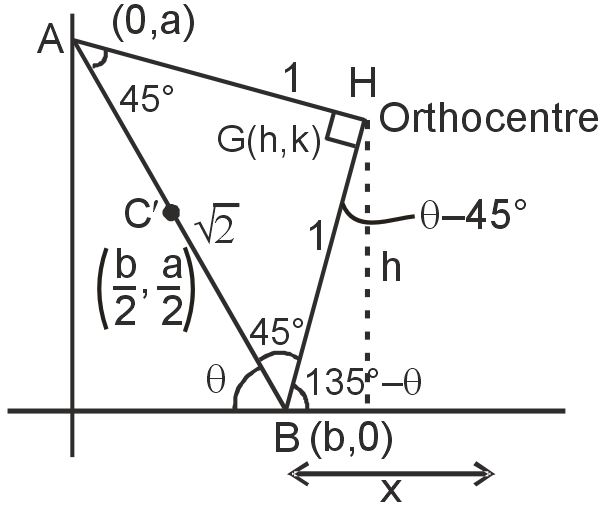
Co-ordinate of orthocenter = b + x = cosθ – =
y-co-ordinate of orthocenter = y1 = 1 . sin(135° – θ)
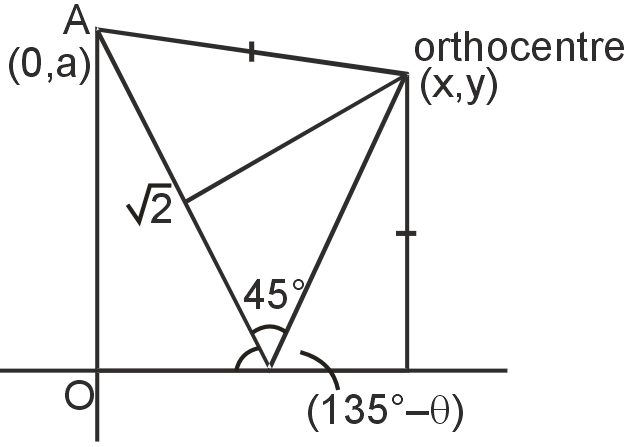
=
∴ ortho.

∴ h = k =
∴ cosθ = 3k – 3sinθ
h =
3 h = 9k – 8sinθ
sinθ = and cosθ =
∴ sin2θ + cos2θ = 1 (h – 3k)2 + (k – 3h)2 = (x – 3y)2 + (y – 3x)2 =