Column-I represents potential energy graph for certain system. Column-II gives statements related to graphs. Column I Column II 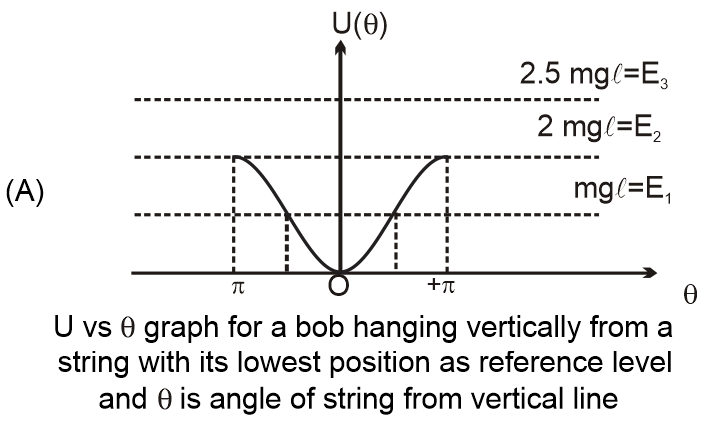(P) If total energy is E3, it is not possible for the body to have any turning point in its motion. 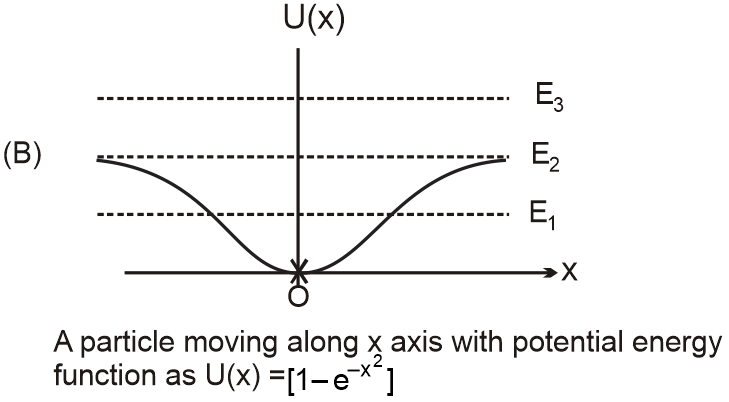(Q) For a small displacement about point O potential energy function is quadratic in variable plotted on x-axis. 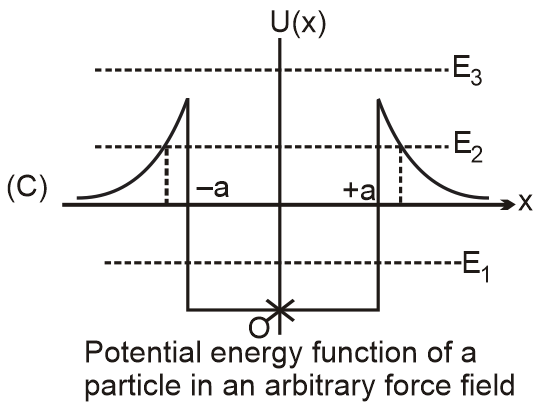(R) For a small displacement about position O motion is simple harmonic. 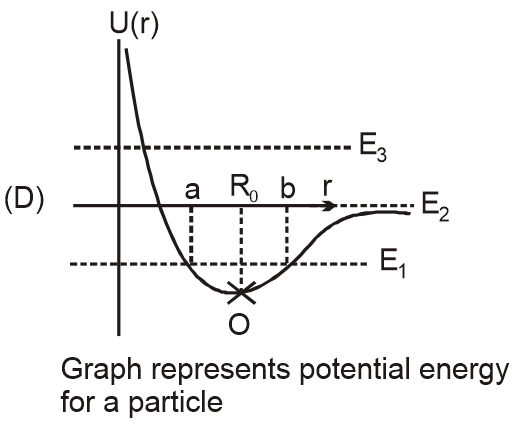(S) If total energy is Etotal < E2 particle executes periodic and oscillatory motion for all energy values greater than energy at O. (T) Point O is position of stable equilibrium

Engineering

Physics

Conservation of Energy

Equilibrium

Basics of Simple Harmonic Motion

Question

Column-I represents potential energy graph for certain system. Column-II gives statements related to graphs.

Column I	Column II
	(P) If total energy is E₃, it is not possible for the body to have any turning point in its motion.
	(Q) For a small displacement about point O potential energy function is quadratic in variable plotted on x-axis.
	(R) For a small displacement about position O motion is simple harmonic.
	(S) If total energy is E_total < E₂ particle executes periodic and oscillatory motion for all energy values greater than energy at O.
	(T) Point O is position of stable equilibrium

LiveFree JEE Main Previous Year Online Papers Live Free JEE Advance Previous Year Online Papers

College PredictorLive

Know your College Admission Chances Based on your Rank/Percentile, Category and Home State.

Get your JEE Main Personalised Report with Top Predicted Colleges in JoSA

This question involves matching potential energy graphs (Column I) with correct physical interpretations (Column II). Key concepts:

Turning points occur where total energy E equals potential energy U. For E₃ in graph 1, U ≤ E everywhere, so no turning points exist (matches P).

Near stable equilibrium (point O in graphs), U is approximately quadratic: $U \approx \frac{1}{2} k x^{2}$ , leading to simple harmonic motion (matches Q, R, T).

For periodic motion, E must be between min(U) and max(U). In graph 4, if E_total < E₂ but > U(O), motion is bounded and oscillatory (matches S).

Final answer: 1-P, 2-QRT, 3-RT, 4-S