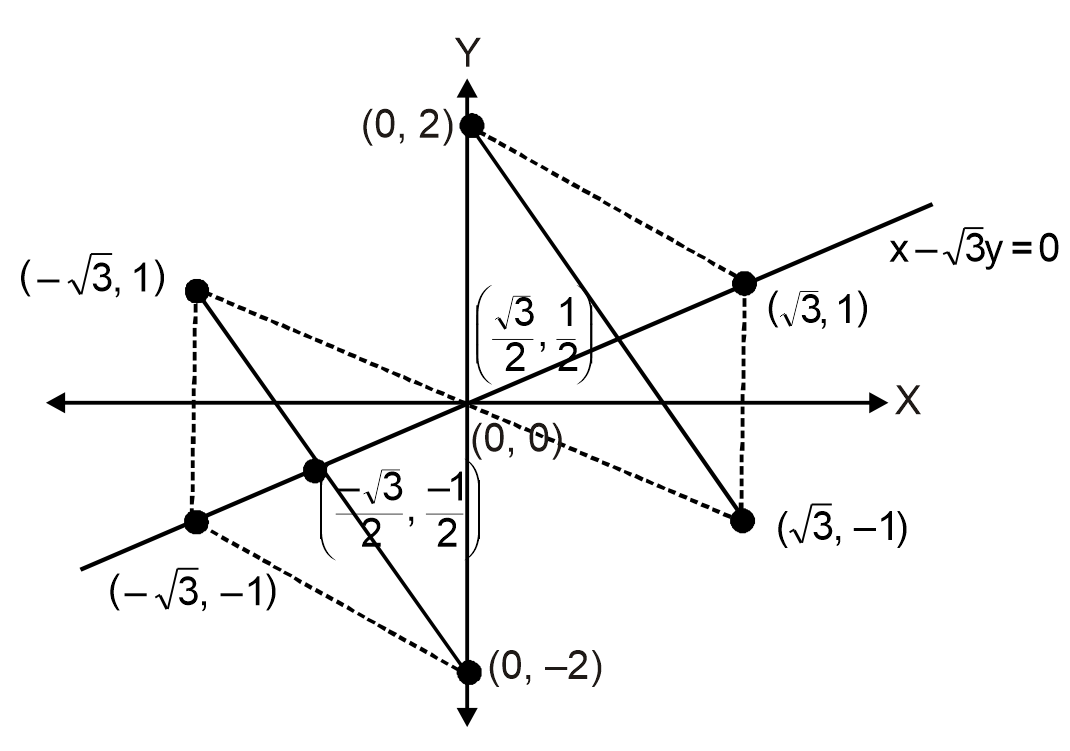
The equation of line $\mathrm{x}-\sqrt{3}\mathrm{y}=0$ in parametric form is 

$\frac{\mathrm{x}-0}{\cos {30}^{\circ }}=\frac{\mathrm{y}-0}{\sin {30}^{\circ }}=\mathrm{r}\Rightarrow \frac{\mathrm{x}-0}{\frac{\sqrt{3}}{2}}=\frac{\mathrm{y}-0}{\frac{1}{2}}=\mathrm{r}$

$\text{ Put }\mathrm{r}=\pm 2\text{, we get }(\sqrt{3},1)\text{ and }(-\sqrt{3},-1)$

Case-1 : Consider two vertices of an equilateral triangle of side 2 as (0, 0) and $(\sqrt{3},1)$.
∴    Equation of line which is perpendicular bisector of (0, 0) and  is $(\sqrt{3},1)$

$\frac{\mathrm{x}-\frac{\sqrt{3}}{2}}{\cos {120}^{\circ }}=\frac{\mathrm{y}-\frac{1}{2}}{\sin {120}^{\circ }}={\mathrm{r}}_1\left(\text{ let }\right)$

$\text{ Put }{\mathrm{r}}_1=\pm \sqrt{3}(\text{ As altitude }=\sqrt{3})$

$\therefore \mathrm{x}=\frac{\sqrt{3}}{2}\pm \sqrt{3}\left(-\frac{1}{2}\right);\mathrm{y}=\frac{1}{2}\pm \sqrt{3}\left(\frac{\sqrt{3}}{2}\right)$

$\Rightarrow \mathrm{x}=\frac{\sqrt{3}}{2}\mp \frac{\sqrt{3}}{2};\mathrm{y}=\frac{1}{2}\pm \frac{3}{2}$

∴Third vertex can be (0, 2) and $(\sqrt{3},-1)$
Case-2 : Consider two vertices of an equilateral triangle of side 2 as (0, 0) and $(-\sqrt{3},-1)$
∴ Equation of line which is perpendicular bisector of (0, 0) and  is $(-\sqrt{3},-1)$

$\frac{\mathrm{x}+\frac{\sqrt{3}}{2}}{\cos {120}^{\circ }}=\frac{\mathrm{y}+\frac{1}{2}}{\sin {120}^{\circ }}={\mathrm{r}}_2\left(\mathrm{let}\right)$

$\text{ Put }\left.{\mathrm{r}}_2=\pm \sqrt{3}\text{ (As altitude }=\sqrt{3}\right)$

$\therefore \mathrm{x}=\frac{-\sqrt{3}}{2}\pm \sqrt{3}\left(\frac{-1}{2}\right);\mathrm{y}=\frac{-1}{2}\pm \sqrt{3}\left(\frac{\sqrt{3}}{2}\right)$

$\Rightarrow \mathrm{x}=\frac{-\sqrt{3}}{2}\mp \frac{\sqrt{3}}{2};\mathrm{y}=\frac{-1}{2}\pm \frac{3}{2}$

∴    Third vertex can be $(-\sqrt{3},1)$ and (0, –2)
Note : Number of possible equilateral triangles are four.