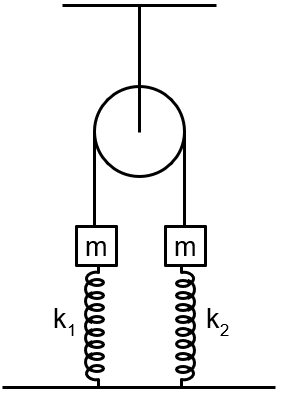
On the diagram, two blocks of equal mass are connected by an ideal string. The values of m = 1kg and k2 = 100 N/m are given. Initially, both springs are relaxed. Then the left block is slowly pulled down a distance 0.1 m and released. Find maximum possible value of k1 (in N/m) for which both the blocks will have same magnitude of acceleration just after releasing. Both spring have natural length of 2m.
Know your College Admission Chances Based on your Rank/Percentile, Category and Home State.
Get your JEE Main Personalised Report with Top Predicted Colleges in JoSA
Let T be the tension in the ideal string and 'a' be the acceleration of the blocks at the instant of release. For the block on the left, the upward acceleration may be found from
T + k1x – mg = ma
For the block on the right, the downward acceleration may be found from
k2x + mg – T = ma
Adding the equations gives the acceleration of the blocks as
a = (k1 + k2)x/(2m)
However, substracting the equations gives
T = mg – (k1 – k2)x/2
for maximum value of k1 T will be zero.
k1 = 300