Question
Superposition Theorem is also used to analyse circuits.
The strategy used in the Superposition Theorem is to eliminate all but one source of power with in a network at a time, using series/parallel analysis to determine voltage drops (and/or currents) within the modified network for each power source separately. Then, once voltage drops and/or currents have been determined for each power source working separately, the values are all "superimposed" on top of each other (added algebraically) to find the actual voltage drops/currents with all sources active. Let's look at a circuit and apply Superposition Theorem to it :
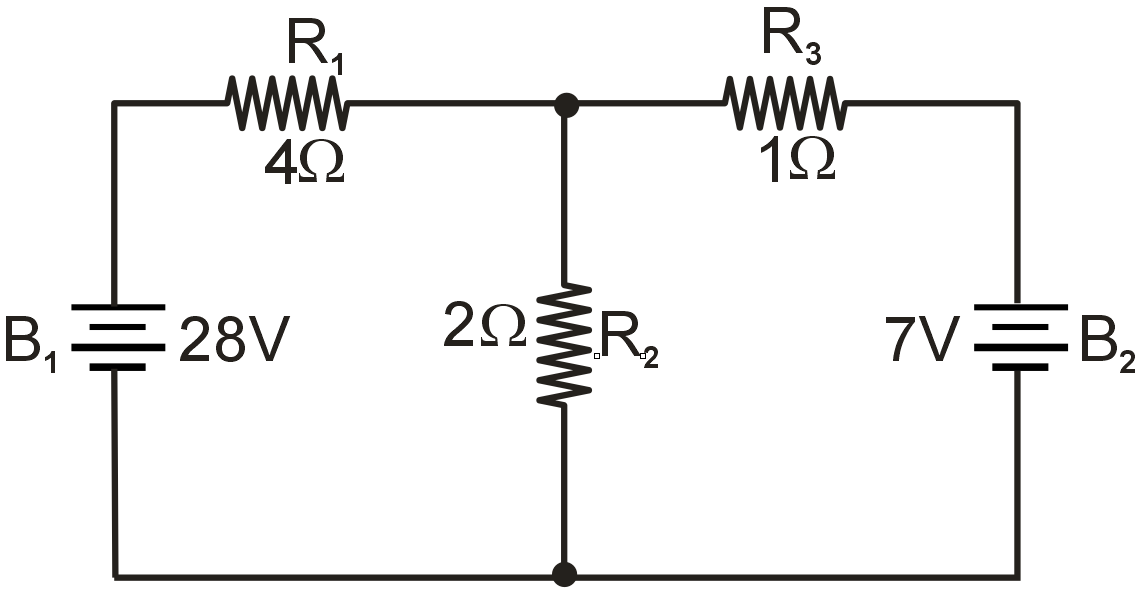
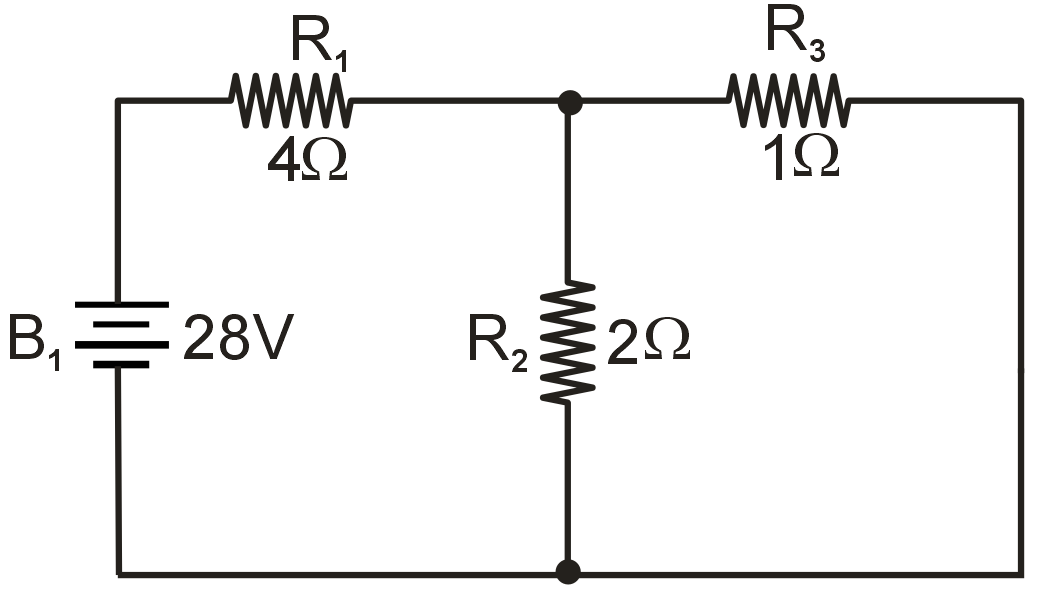
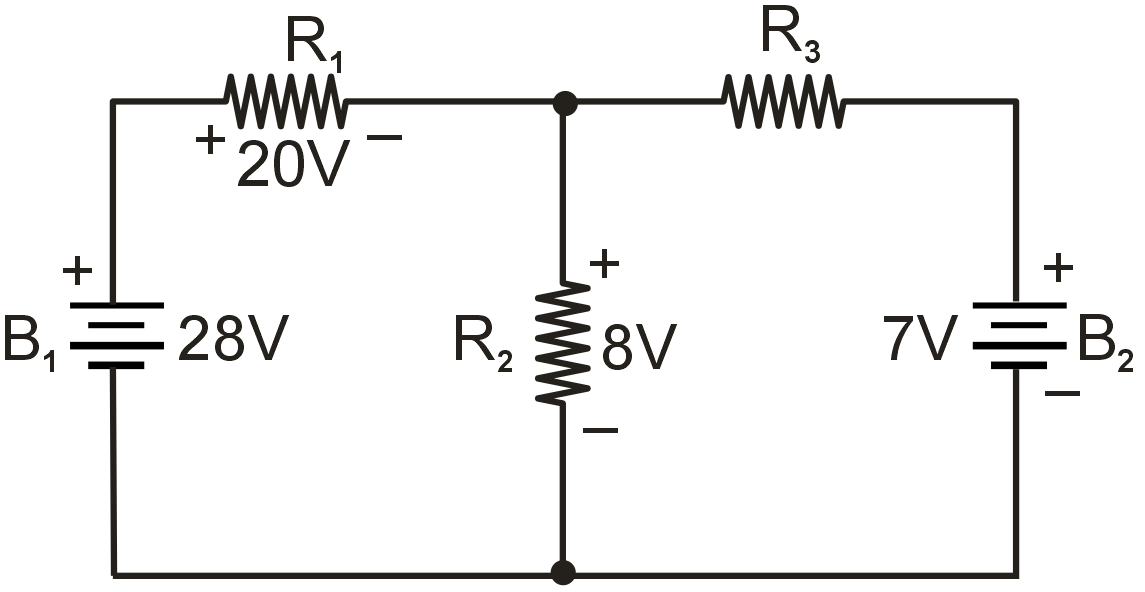
Since we have two sources of power in the circuit, we will have to calculate two sets of values for voltage drops, one for the circuit with only the 28 volt battery in effect ...
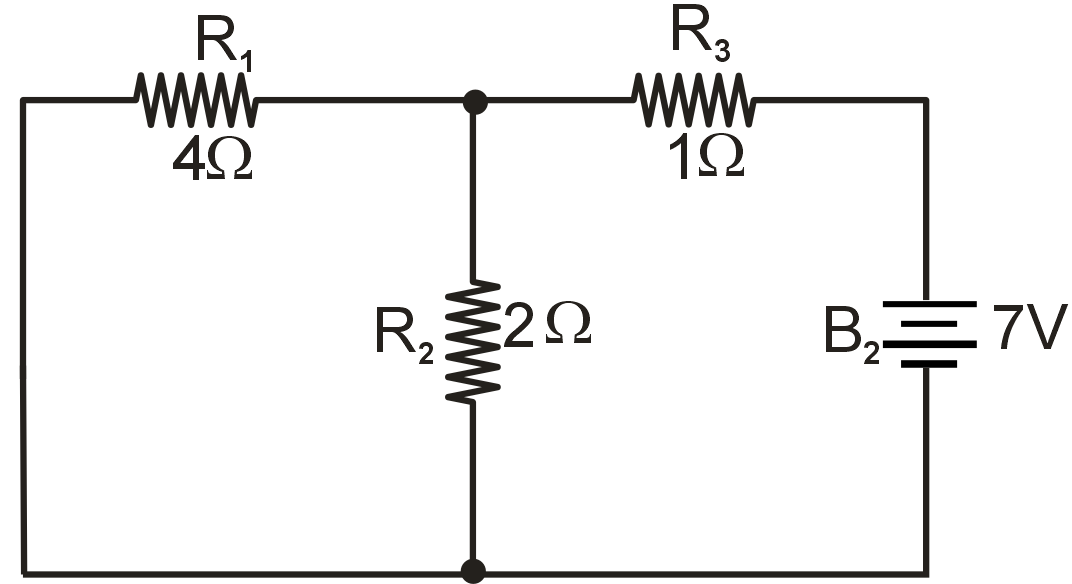
...... and one for the circuit with only the 7 volt battery in effect :
When re-drawing the circuit for series/parallel analysis with one source, all other voltage sources are replaced by wire (shorts).
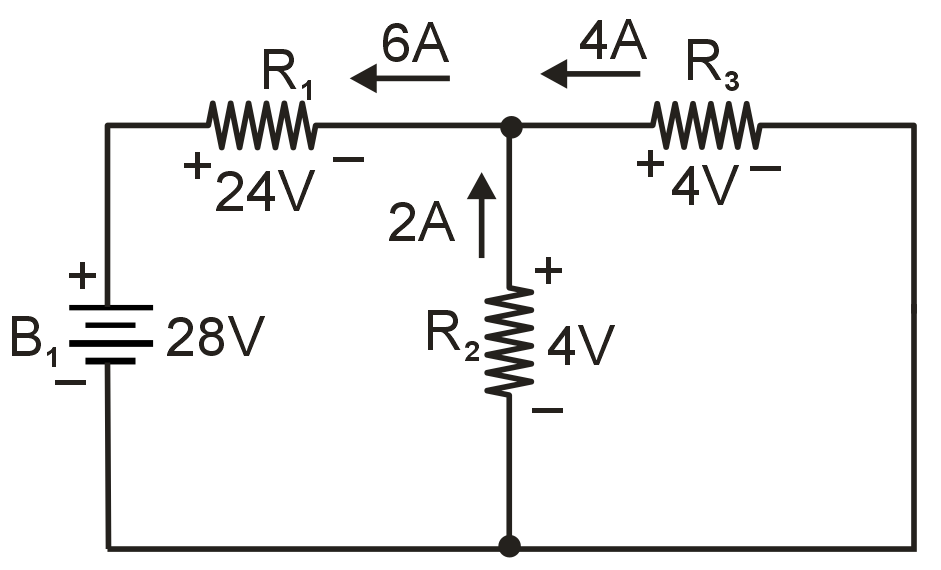
Analyzing the circuit with only the 28 volt battery, we obtain the following values for voltage and current:
Analyzing the circuit with only the 7 volt battery, we obtain another set of values for voltage and current:
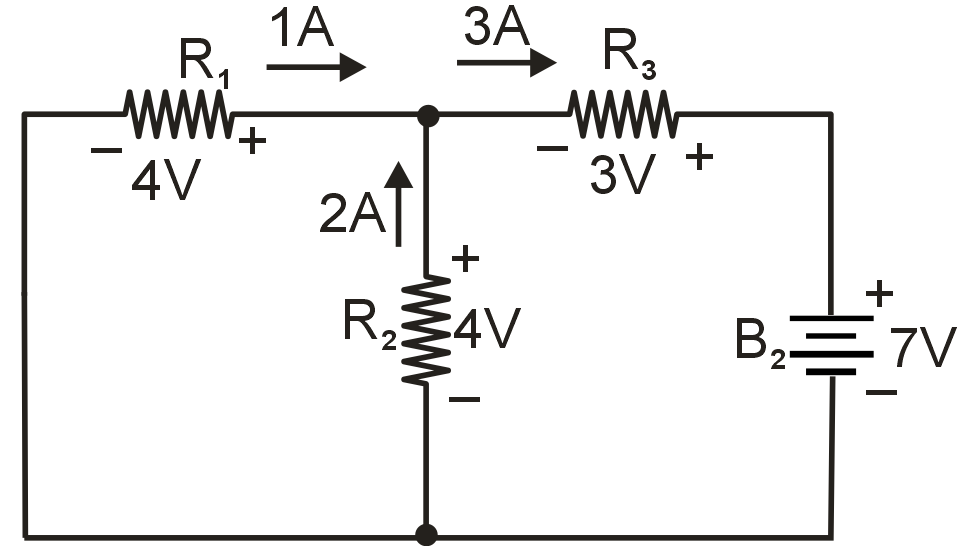
When superimposing these values of voltage and current, we have to be very careful to consider polarity (voltage drop) and direction (electron flow), as the values have to be added algebraically, Applying these superimposed voltage figures to the circuit, the end result looks something like this :
Currents add up algebraically as well, and can either be superimposed as done with the resistor voltage drops, or simply calculated from the final voltage drops and respective resistances (I = E/R). Either way, the answer will be the same.
It must be noted, though, that the Superposition Theorem works only for circuits that are reducible to series/parallel combinations for each of the power sources at a time (thus, this theorem is useless for analyzing an unbalanced bridge circuit), and it only works where the underlying equations are linear (no mathematical powers or roots). The requisite of linearity means that Superposition Theorem is only applicable for determining voltage and current, not power !!! Power dissipations, being nonlinear functions, do not algebraically add to an accurate total when only one source is considered at a time. The need for linearity also means this Theorem cannot be applied in circuits where the resistance of a component changes with voltage or current. Hence, networks containing components like lamps (incandescent or gas-discharge) or varistors could not be analyzed.
Know your College Admission Chances Based on your Rank/Percentile, Category and Home State.
Get your JEE Main Personalised Report with Top Predicted Colleges in JoSA
In which of the following cases, the current through the element can be analysed with superposition principle.
(i) Battery with internal resistance.
(ii) An element for which voltage versus current is 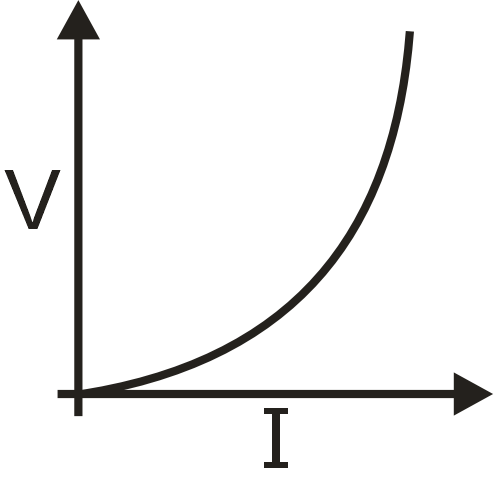
(iii) An element for which voltage versus current is 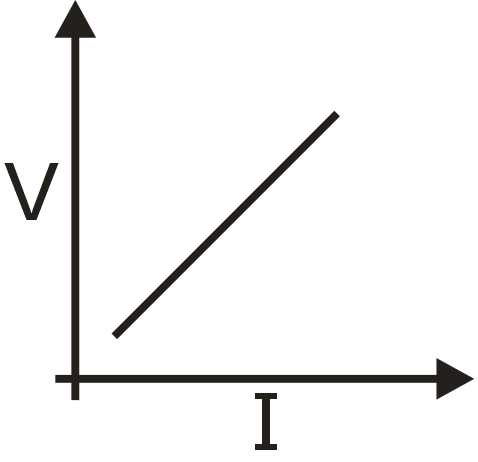
(iv) Resistors for which power dissipated varies directly as square of the current.
no solution
In the question, the total potential drop across R3 will be :
= A drop in potential of 1V
If we want to find power dissipated in any resistor when using battery-1 gives power dissipated as P1 and battery-2 gives power dissipated as P2, we should use.
P = (i1 + i2)2 R = P1 + P2 +