Question
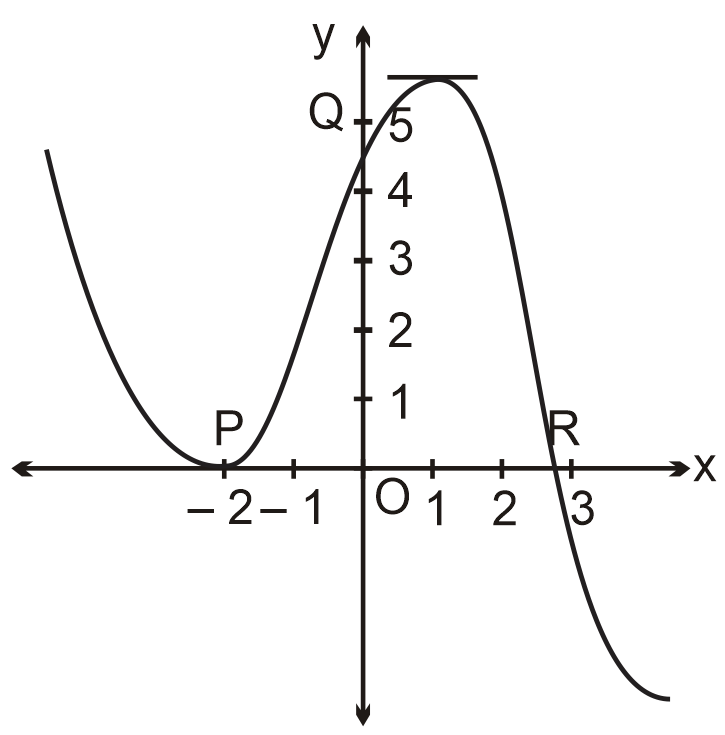
The graph of a polynomial f(x) of degree 3 is as shown in the figure and slope of tangent at Q (0, 5) is 3.
Know your College Admission Chances Based on your Rank/Percentile, Category and Home State.
Get your JEE Main Personalised Report with Top Predicted Colleges in JoSA
Area bounded by the curve y = f(x) with x axis and lines x + 1 = 0, x – 1 = 0 is
Let f(x) = ax3 + bx2 + cx + d
∴ f(0) = 5 ⇒ d = 5
So, f(x) = ax3 + bx2 + cx + 5
∴ f '(x) = 3ax2 + 2bx + c
Now, f '(–2) = 0 ⇒ 12a – 4b + c = 0 .....(1)
and y = f(x) passes through P (–2, 0), so 0 = – 8a + 4b – 2c + 5 ......(2)
Also, f '(0) = 3 ⇒ c = 3 .....(3)
∴ On solving, we get a
Required area
The equation of normal at the point where curve crosses y-axis, is
Let f(x) = ax3 + bx2 + cx + d
∴ f(0) = 5 ⇒ d = 5
So, f(x) = ax3 + bx2 + cx + 5
∴ f '(x) = 3ax2 + 2bx + c
Now, f '(–2) = 0 ⇒ 12a – 4b + c = 0 .....(1)
and y = f(x) passes through P (–2, 0), so 0 = – 8a + 4b – 2c + 5 ......(2)
Also, f '(0) = 3 ⇒ c = 3 .....(3)
∴ On solving, we get a
Equation of normal at Q(0, 5) is
Number of solutions of the equation |f(|x|)| = 3, is
Let f(x) = ax3 + bx2 + cx + d
∴ f(0) = 5 ⇒ d = 5
So, f(x) = ax3 + bx2 + cx + 5
∴ f '(x) = 3ax2 + 2bx + c
Now, f '(–2) = 0 ⇒ 12a – 4b + c = 0 .....(1)
and y = f(x) passes through P (–2, 0), so 0 = – 8a + 4b – 2c + 5 ......(2)
Also, f '(0) = 3 ⇒ c = 3 .....(3)
∴ On solving, we get a
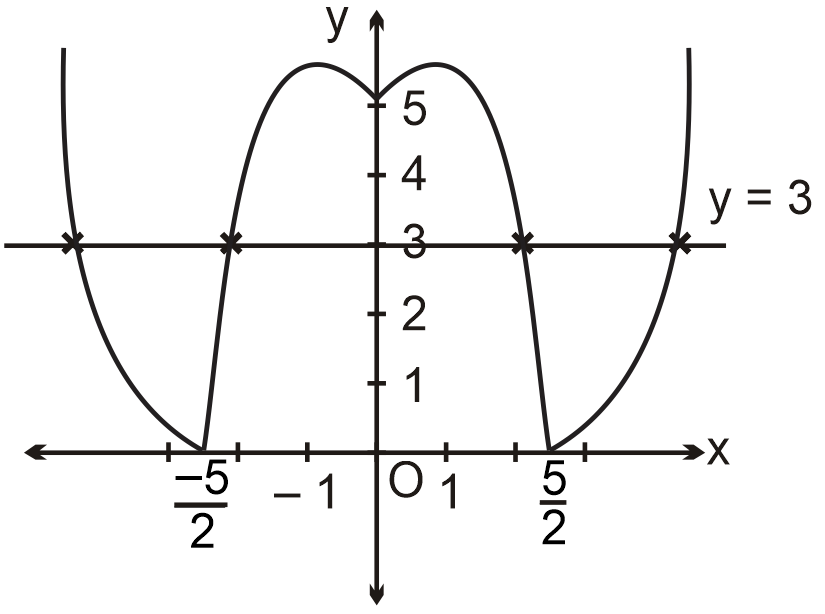
Clearly, from above graph, we get, number of solutions of equation |f(|x|)| = 3 are 4.