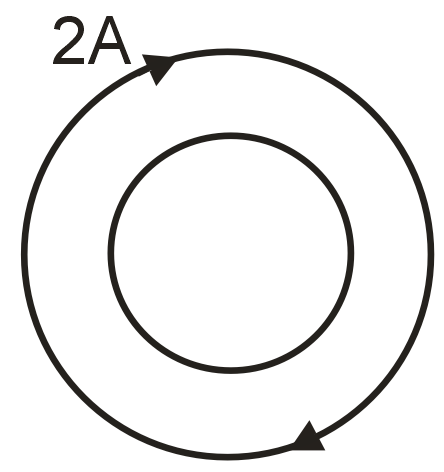
Two unconnected circular loops of wire lie in the same plane with the same centre, as shown in the diagram. The outerloop carries current of 2A in a clockwise direction and has twice the radius of the inner loop. If the magnetic field at the centre of the loops is zero, then the current in the inner loop must be :

Engineering

Physics

Magnetic Field

Biot Savart Law

Amperes Circuital Law and its Applications

Question

Two unconnected circular loops of wire lie in the same plane with the same centre, as shown in the diagram. The outerloop carries current of 2A in a clockwise direction and has twice the radius of the inner loop. If the magnetic field at the centre of the loops is zero, then the current in the inner loop must be :

1A in the clockwise direction

2A in the clockwise direction

1A in the counterclockwise direction

2A in the counterclockwise direction

LiveFree JEE Main Previous Year Online Papers Live Free JEE Advance Previous Year Online Papers

College PredictorLive

Know your College Admission Chances Based on your Rank/Percentile, Category and Home State.

Get your JEE Main Personalised Report with Top Predicted Colleges in JoSA

The magnetic field at the center of a circular loop is given by B = (μ₀I)/(2R). For the net field to be zero, the fields from both loops must be equal in magnitude and opposite in direction.

The outer loop (radius 2R, current 2A clockwise) produces a field: $B_{outer} = \frac{μ_{0} \times 2}{2 \times 2 R} = \frac{μ_{0}}{2 R}$ into the page (clockwise current).

To cancel this, the inner loop (radius R) must produce a field of equal magnitude out of the page. This requires a counterclockwise current. Solving for I: $\frac{μ_{0} I}{2 R} = \frac{μ_{0}}{2 R}$ , so I = 1A.

Final Answer: 1A in the counterclockwise direction